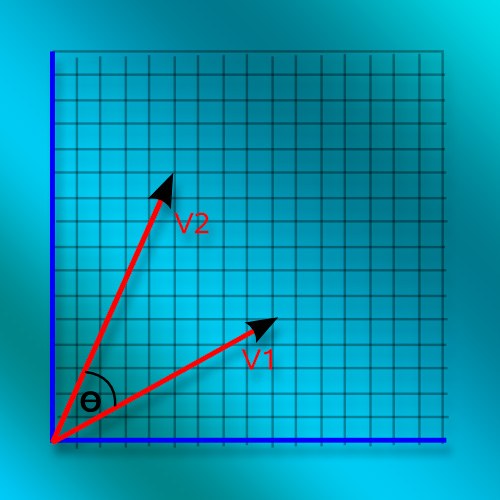
टिप 1: सूर्य के प्रकाश की घटनाओं के कोण को कैसे तय किया जाए
टिप 1: सूर्य के प्रकाश की घटनाओं के कोण को कैसे तय किया जाए
अलग-अलग में एक ही भौगोलिक बिंदु परदिन का समय, सूरज की किरणें विभिन्न कोणों से पृथ्वी पर आती हैं इस कोण की गणना और भौगोलिक निर्देशांक जानने के लिए, आप खगोलीय समय की सही गणना कर सकते हैं। शायद विपरीत प्रभाव सटीक खगोलीय समय को दर्शाता है एक कालमीटर का प्रयोग करके, आप भू-संदर्भित कर सकते हैं।

आपको आवश्यकता होगी
- - जीनोमोन;
- - शासक;
- - क्षैतिज सतह;
- - एक क्षैतिज सतह स्थापित करने के लिए तरल स्तर;
- - कैलकुलेटर;
- - स्पर्शरेखा और कोटानेंट्स के टेबल
अनुदेश
1
कड़ाई से क्षैतिज सतह खोजें इसे एक स्तर के साथ देखें आप एक बुलबुला और एक इलेक्ट्रॉनिक उपकरण दोनों का उपयोग कर सकते हैं। यदि आप तरल स्तर का उपयोग करते हैं, तो बबल कड़ाई से केंद्र में होना चाहिए। अधिक काम की सुविधा के लिए, सतह पर कागज की एक शीट तय करें इस मामले में ग्राफ पेपर का उपयोग करना सबसे अच्छा है। एक क्षैतिज सतह के रूप में, आप मोटी, ठोस प्लाईवुड की एक शीट ले सकते हैं। इसमें किसी भी अवसाद या पहाड़ी नहीं होना चाहिए।
2
ग्राफ़ पेपर पर कोई बिंदु या क्रॉस बनाएं। गनोमोन खड़ी रूप से सेट करें ताकि इसकी धुरी आपके निशान के साथ मेल खाता हो। एक गोोनोमोन एक कड़ाई से तय रॉड या पोल है। इसके शीर्ष में एक तीव्र शंकु का आकार होता है
3
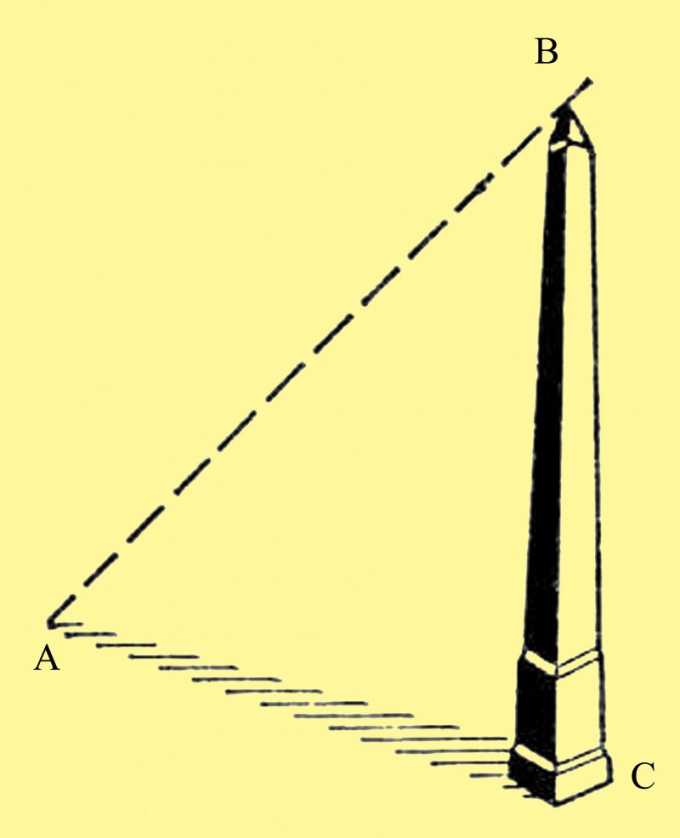
गुमनाम छाया के अंत बिंदु पर, दूसरे स्थान पर रखेंबिंदु। इसे बिंदु ए के रूप में निर्दिष्ट करें, और बिंदु सी के रूप में पहले। गुंजाइश की ऊंचाई पर्याप्त सटीकता के साथ आपको जानी जानी चाहिए। गुंजाइम जितना बड़ा होता है, उतना सटीक होगा परिणाम।
4
बिंदु ए से दूरी को किसी भी सी से इंगित करेंआप के लिए सुलभ ध्यान दें कि माप की इकाइयां गुमानों की ऊंचाई के समान हैं यदि आवश्यक हो, तो सबसे सुविधाजनक इकाइयों में अनुवाद करें।
5
कागज की एक अलग शीट पर, एक चित्र खींचें,प्राप्त डेटा का उपयोग करना। ड्राइंग में, एक आयताकार त्रिभुज प्राप्त किया जाना चाहिए, जिसमें सही कोण सी है gnomon स्थापना स्थान, सीए छाया की लंबाई है, और SW चार्ट गुंजाइम की ऊंचाई है
6
सूत्र टीजीए = बीसी / एसी का उपयोग करते हुए स्पर्शरेखा या कोटयेंट की मदद से कोण A की गणना करें स्पर्शरेखा को जानने के लिए, कोण स्वयं को निर्धारित करें
7
परिणामस्वरूप कोण क्षैतिज सतह और सूरज की किरण के बीच का कोण है। घटना के कोण सतह के किनारे के बीच का कोण और रे है यही है, यह 90 डिग्री- ए के बराबर है
टिप 2: एक बिंदु से एक सीधी रेखा तक की दूरी निर्धारित करने के तरीके
से दूरी निर्धारित करने के लिए बिंदु अप करने के लिए सीधे यह समीकरणों को जानना आवश्यक है सीधे और निर्देशांक बिंदु कार्टेशियन समन्वय प्रणाली में दूरी से बिंदु अप करने के लिए सीधे इस से खींचा सीधा होगा बिंदु को सीधे.

आपको आवश्यकता होगी
- बिंदु के निर्देशांक और रेखा के समीकरण
अनुदेश
1
सामान्य समीकरण सीधे कार्टेशियन निर्देशांक में एक्स + बाय + सी = 0 का फ़ॉर्मेट है, जहां ए, बी और सी संख्या ज्ञात हैं। इस बिंदु को O को कर्टेशियन समन्वय प्रणाली में निर्देशांक (x1, y1) निर्देशित करना चाहिए। इस मामले में, इस का विचलन बिंदु से सीधे के बराबर है? = (Ax1 + By1 + C) / sqrt ((A ^ 2) + (B ^ 2)) यदि सी <0, और? (= Ax1 + By1 + C) / (- sqrt ((एक ^ 2 ) + (बी ^ 2))) यदि सी> 0 से दूरी बिंदु अप करने के लिए सीधे विचलन मॉड्यूल है बिंदु से सीधे, जो है, आर = | (Ax1 + By1 + C) / sqrt ((एक ^ 2) + (बी ^ 2)) | यदि सी <0, और? = | (Ax1 + By1 + C) / (- sqrt ((ए ^ 2) + (बी ^ 2))) | सी सी 0
2
अब निर्देशांक के साथ बिंदु दें (x1, y1, z1)तीन-आयामी अंतरिक्ष में दिया गया है एक पंक्ति को तीन समीकरणों की एक प्रणाली द्वारा पैरामीट्रिक रूप से निर्दिष्ट किया जा सकता है: x = x0 + ta, y = y0 + tb, z = z0 + tc, जहां टी एक वास्तविक संख्या है से दूरी बिंदु अप करने के लिए सीधे इस से न्यूनतम के रूप में पाया जा सकता है बिंदु मनमाना करने के लिए बिंदु सीधे। इसके गुणांक टी बिंदु tmin = (a (x1-x0) + b (y1-y0) + c (z1-z0)) / ((एक ^ 2) + (बी ^ 2) + (c ^ 2) के बराबर है)
3
से दूरी बिंदु (x1, y1) करने के लिए सीधे यह भी गणना की जा सकती है अगर सीधी रेखा को कोणीय गुणांक वाले समीकरण से दिया जाता है: y = kx + b फिर समीकरण को यह सीधा सीधे का रूप होगा: y = (-1 / k) x + a इसके बाद, आपको इस बात को ध्यान में रखना होगा कि इस रेखा को बिंदु (एक्स 1, वाई 1) से गुजरना होगा। इसलिए संख्या एक परिवर्तन के बाद, बिंदु के बीच की दूरी और सीधे.