एक सदिश की दिशा cosines कैसे खोजने के लिए

एक सदिश की दिशा cosines कैसे खोजने के लिए



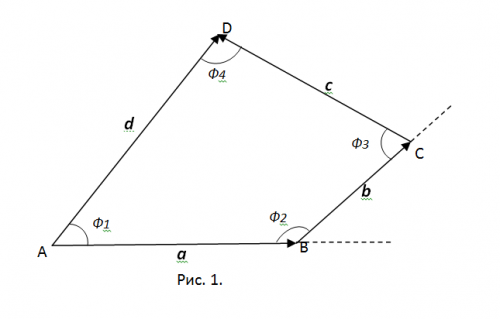
एल्फा, बीटा और गामा द्वारा वेक्टर द्वारा गठित कोणों को निर्देशांक अक्षों की सकारात्मक दिशा के साथ निरूपित करें (चित्र 1 देखें)। कोज्या इन कोणों को दिशा cosines कहा जाता है वेक्टर एक।





एक सदिश की दिशा cosines कैसे खोजने के लिए


















आपको आवश्यकता होगी




  • - कागज;
  • - संभाल




अनुदेश





1


चूंकि किसी कार्टेशियन आयताकार समन्वय प्रणाली में समन्वय करता है, इसलिए अनुमानों के बराबर हैं वेक्टर समन्वय अक्षों पर, फिर a1 = | a | cos (अल्फा), a2 =| एक | क्योंकि (बीटा), a3 = | एक | cos (गामा)। इसलिए: क्योंकि (अल्फा) = A1 || एक |, क्योंकि (बीटा) = A2 || एक |, क्योंकि (गामा) = a3 / | एक |। इस मामले में, | एक | = sqrt (A1 ^ 2 + A2 ^ 2 + a3 ^ 2)। क्योंकि (अल्फा) तो = A1 | sqrt (A1 ^ 2 + A2 ^ 2 + a3 ^ 2), क्योंकि (बीटा) = A2 | sqrt (A1 ^ 2 + A2 ^ 2 + a3 ^ 2), क्योंकि (गामा) = a3 / sqrt (A1 ^ 2 + A2 ^ 2 + a3 ^ 2)।





2


यह कोसिंस निर्देशन की बुनियादी संपत्ति पर ध्यान दिया जाना चाहिए। दिशा cosines के वर्गों का योग वेक्टर एकता के बराबर है। दरअसल, cos2 (अल्फा) + cos2 (बीटा) + cos2 (गामा) = a1 ^ 2 | (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) + ए 2 ^ 2 | ( a1 ^ 2 + a2 ^ 2 + a3 ^ 2) + a3 ^ 2 / (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) = (a1 ^ 2 + a2 ^ 2 + a3 ^ 2) | (ए 1 ^ 2 + ए 2 ^ 2 + ए 3 ^ 2) = 1





3


पहला तरीका उदाहरण: दिए गए: वेक्टर ए = {1, 3, 5)। यह गाइड kosinusy.Reshenie का पता लगाएं। एक | | = sqrt (कुल्हाड़ी ^ 2 + ay ^ 2 + az ^ 2) = sqrt (1 + 9 +25) = sqrt (35) = 5.91: पाया लिखने बाहर के अनुसार। इस प्रकार, प्रतिक्रिया निम्न रूप में लिखा जा सकता है: {क्योंकि (अल्फा), क्योंकि (बीटा), क्योंकि (गामा)} = {1 / sqrt (35) और 3 / sqrt (35), 5 / (35)} = { 0.16, 0.5, 0.84}।





4


दूसरा रास्ता जब दिशा cosines ढूँढने वेक्टर एक, आप एक स्केलर उत्पाद का उपयोग करके कोनों के cosines निर्धारित करने की तकनीक का उपयोग कर सकते हैं। इस मामले में, दिमाग में व्यक्ति की दिशा और एक के बीच का कोण होता है वेक्टरआयताकार कार्टेशियन निर्देशांक i, j, और k उनके निर्देशांक क्रमशः {1, 0, 0}, {0, 1, 0}, 0, 0, 1} हैं। इसे याद किया जाना चाहिए कि वैक्टर के स्केलर उत्पाद को इस प्रकार परिभाषित किया गया है। यदि बीच के कोण वेक्टरतो दो हवाओं के स्केलर उत्पाद (इनपरिभाषा) एक संख्या है जो कि कॉस के द्वारा वैक्टर के मॉड्यूल के उत्पाद के बराबर है। (ए, बी) = | एक || बी | कॉस φ उसके बाद, यदि बी = आई, तब (ए, आई) = | एक || आई | कॉस (अल्फा), या ए 1 = | ए | कॉस (अल्फा) इसके अलावा, सभी क्रियाएं विधि 1 के रूप में उसी तरीके से की जाती हैं, जो जम्मू और कश्मीर के निर्देशांक को ध्यान में रखते हैं।




























0